4.1 Röntgendiffraktometrie

Die Bestimmung der Kristallstruktur einer Verbindung und deren Gitterkonstanten geschieht mit der Röntgenpulverdiffraktometrie nach dem Debye-Scherrer-Verfahren. Nähere Informationen zu diesem Kapitel siehe [Ashcroft76].

Kristallstrukturen

Im Kristall sind die einzelnen Atome periodisch in einem Gitter angeordnet. Zu jedem Kristallgitter läßt sich eine Einheitszelle finden, aus der das Gitter aufgebaut ist und die die volle Symmetrie dieses Gitters repräsentiert. Handelt es sich beispielsweise um ein orthorhombisches Kristallgitter, so ist die Einheitszelle ein Quader mit den Kantenlängen a, b und c, den Gitterkonstanten.

Insgesamt sind sieben solcher Kristallsysteme denkbar: kubisch, tetragonal, orthorhombisch, monoklin, triklin, trigonal und hexagonal. Die ersten vier lassen sich weiter unterteilen, so daß man insgesamt vierzehn sogenannte Bravais-Gitter unterscheiden kann. Innerhalb der einzelnen Gitter stellt man anhand der möglichen Symmetrieoperationen, die das Gitter wieder auf sich selbst abbilden, eine Klassifizierung nach verschiedenen Raumgruppen her. Dabei sucht man beispielsweise nach Dreh- und Spiegelachsen oder nach Inversionspunkten. Man kann zeigen, daß es genau 230 verschiedene Raumgruppen gibt.

Eine Nomenklatur für die Kristallstrukturen ergibt sich z.B. aus dem zugrundeliegenden Bravais-Gitter in Verbindung mit der Anzahl der in der Einheitszelle enthaltenen Atome. Dies ist die sogenannte Pearson-Notation [Pearson85]. So bedeutet beispielsweise "tI10" ein tetragonal innenzentriertes Kristallgitter mit zehn Atomen pro Einheitszelle. Eine zweite Möglichkeit ist die internationale Notation, die sich an den Symmetrieoperationen des Gitters orientiert. Hier bedeutet "", oder abgekürzt "I4/mmm", die Existenz einer vierzähligen Rotationsachse in einem raumzentrierten ("I ") Gitter mit dazu senkrechter (angedeutet durch den Bruchstrich) Spiegelebene ("m" steht für "mirror"), die zwei weitere zweizählige Rotationsachsen und jeweils dazu senkrechten Spiegelebenen enthält.

Tabelle 4.1 zeigt eine Übersicht der wichtigen in ternären Ytterbium-Verbindungen vorkommenden Kristallstrukturen. In Kapitel 5 sind die Abbildungen zu diesen Strukturen zu finden.
Name der Struktur anderer Name  Pearson-Symbol Raumgruppe  Symmetrie Abbildung Beispiele 
W2B2Co Mo2B2Ni  oI10 71 Immm  Bild Yb2Ni2Al 
ThCr2Si2 Al4Ba  tI10 139 I4/mmm  Bild YbCo2Ge2 
BiF3 MnCu2Al  cF16 225 Fmm  Bild YbNi2Sn 
TiNiSi Co2Si oP12 62 Pnma Bild YbPtAl, YbNiGa
MgCuAl2 BRe3  oC16 63 Cmcm  Bild YbNiGa2, YbPtGa2 
ZrNiAl Fe2P hP9 189 P2m  Bild YbNiAl
Y2Co3Ga9 - oC56 63 Cmcm Bild Yb2Ir3Al9 
Tabelle 4.1: Einige Kristallstrukturen von ternären Ytterbium-Verbindungen.

Zu den die Einheitszelle aufspannenden Vektoren a, b und c definiert man das sogenannte reziproke Gitter mit den Basisvektoren a*, b* und c* durch

usw., wobei V das Volumen der Einheitszelle ist und b × c das äußere Produkt der Vektoren b und c. Man kann zeigen, daß jede ganzzahlige Linearkombination der Vektoren des reziproken Gitters senkrecht auf einer Familie von Gitternetzebenen des realen Gitters steht. Dies ist eine Schar äquidistanter Ebenen, die periodisch angeordnet zusammen alle Punkte des Gitters enthalten. Die Koeffizienten dieser Linearkombination sind die sogenannten Millerschen Indizes (h k l).

Das Debye-Scherrer-Verfahren

Monochromatisches Röntgenlicht trifft im Winkel q auf einen Kristall, von dessen Gitternetzebenen es reflektiert wird. Es kommt zu konstruktiver Interferenz, wenn q die Bragg-Bedingung

erfüllt, wobei d der Abstand der Gitternetzebenen ist, l die Wellenlänge der einfallenden Röntgenstrahlung und n die Ordnung der Interferenz. Die Intensität des reflektierten Strahls wird unter dem Winkel 2q mit einem Detektor gemessen. Verstellt man die Winkel q und 2q des ein- und ausfallenden Röntgenstrahls über einen größeren Bereich, so erhält man das für die Substanz charakteristische, aus zahlreichen Peaks unterschiedlicher Intensität bestehende Diffraktogramm. Die Position der einzelnen Peaks wird dabei von den Gitterkonstanten bestimmt, die relativen Intensitäten jedoch von den Formfaktoren der einzelnen Atome. Die einzelnen Peaks lassen sich bei Kenntnis der Kristallstruktur den Millerschen Indizes (h k l) zuordnen und aus deren Lage die Gitterkonstanten bestimmen. Für rechtwinklige bzw. hexagonale Kristallgitter gelten die Beziehungen:

bzw. .

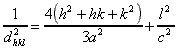Dabei sind dhkl der den jeweiligen (h k l)-Werten entsprechende Abstand der Gitternetzebenen sowie a, b und c die Gitterkonstanten.

Aufnahme des Diffraktogramms

Ein kleiner Teil der Probe (etwa 2 mm2) wird abgesägt und in einem Wolframkarbid-Mörser zu Pulver zermahlen. Das Pulver wird mit Zaponlack, der selbst auf dem späteren Diffraktogramm aufgrund seiner amorphen Struktur nicht zu sehen ist, auf einem Objektträger aus Acryl oder Glas fixiert. Mit einem Zweikreis-Röntgendiffraktometer der Firma Siemens (eine Beschreibung der Anlage ist in [Thies91]) erfolgt die Messung im Bereich 10° < 2q < 90° vollautomatisch. Die Wellenlänge der verwendeten Cu-Ka1-Strahlung beträgt 1,54056 Å und die Anodenspannung typisch 35 kV bei einem typischen Strom von 5 - 35 mA. Bei bekannter Struktur erfolgt die Bestimmung der Gitterkonstanten mit der vorhandenen Software mit einer Genauigkeit von besser als 1 ‰.

Fremdphasen

Neben der Kristallstruktur läßt sich mit der Röntgenpulverdiffraktometrie der Fremdphasengehalt einer Probe bestimmen. Obgleich sich die Art der Fremdphase mit dieser Methode oftmals nicht bestimmen läßt, ist sie erfahrungsgemäß spätestens ab einem Anteil von etwa 5 % an der Probe im Diffraktogramm sichtbar [Schank94]. Für die Bestimmung ihres relativen Anteils ist die integrale Intensität ihrer Peaks im Diffraktogramm von Bedeutung. Ein ungenaues aber oft brauchbares Maß hierfür ist das Verhältnis der Höhe des größten Peaks der Fremdphase zu der des größten Peaks der Hauptphase, das sich im Gegensatz zu letzterer leicht bestimmen läßt. Abbildung 4.1 zeigt als Beispiel das Röntgendiffraktogramm einer für 120 Stunden bei 600 °C getemperten YbNi2Sn-Probe. Der Vergleich mit einem simulierten Diffraktogramm für diese Verbindung zeigt die Existenz einiger strukturfremder Peaks. Der größte Teil dieser Peaks konnte den Fremdphasen YbNiSn, das in der orthorhombischen TiNiSi-Struktur kristallisiert, YbNi4Sn, das wie YbNi2Sn kubisch ist, und Ni3Sn, das in einer kubischen Hochtemperaturphase existiert und nur einen starken Röntgenpeak zeigt, zugeordnet werden, nachdem deren Diffraktogramme ebenfalls simuliert wurden (ohne Abbildung). Die restlichen zwei konnten keiner Struktur zugeordnet werden. Der relative Anteil aller Fremdphasen in dieser Probe beträgt aus den Peakhöhenverhältnissen etwa 10 %.
Kapitel 4