2.2 Die Theorie der Schwere-Fermionen-Systeme
Die Schwere-Fermionen-Systeme haben ihren Namen von der stark erhöhten
effektiven Masse der für die physikalischen Eigenschaften verantwortlichen
Quasiteilchen. Diese sind Anregungszustände der Leitungselektronen,
die wie alle Teilchen mit halbzahligem Spin der Fermi-Dirac-Statistik unterliegen
und daher Fermionen genannt werden. Der folgende Abschnitt widmet sich
einem kurzen Einblick in die theoretische Beschreibung des Verhaltens dieser
Systeme.
Metalle der Seltenen Erden
Die Seltenen Erden sind Scandium, Yttrium, Lanthan und die sogenannten
Lanthaniden. Als solche bezeichnet man die im Periodensystem der Elemente
hinter Lanthan folgenden Elemente mit den Ordnungszahlen 58 - 71. Bei den
Lanthaniden wird die 4f-Schale sukzessive mit Elektronen aufgefüllt.
Die f-Schalen der Seltenen Erden tragen ein magnetisches Moment, wenn sie
nicht vollständig gefüllt sind oder leer. Die Besonderheit der
f-Wellenfunktion ist, daß sie sehr nahe am Atomkern lokalisiert ist.
In metallischen Verbindungen besitzen die 4f-Wellenfunktionen der Selten-Erd-Ionen
daher praktisch keinen Überlapp mit den Wellenfunktionen der Liganden.
Valenz-Instabilitäten in Selten-Erd-Verbindungen
Bei den Seltenen Erden Cer, Ytterbium und Europium liegen mehrere Elektronenkonfigurationen
energetisch sehr dicht beieinander. Die Lanthaniden sind in der Regel dreiwertig,
d.h. sie geben die drei (5d6s2)-Elektronen an das Leitungsband
ab. Die 4f-Elektronen bleiben davon unberührt. Oft führt aber
die Abgabe oder Aufnahme eines Elektrons in die 4f-Schale zu einer größeren
Energieabsenkung. Das Selten-Erd-Ion ist dadurch vier- oder zweiwertig.
In Verbindungen kann es auch energetisch günstig sein, wenn Elektronen
zwischen dem Leitungsband und den f-Schalen fluktuieren, so daß die
Selten-Erd-Ionen im zeitlichen Mittel keine ganzzahlige Valenz besitzen.
Man spricht in diesem Fall von zwischenvalentem Verhalten. Der Effekt wird
auch als Valenz- oder 4f-Instabilität bezeichnet. Die Valenzfluktuationen
verhindern die Bildung eines stabilen magnetischen Moments, und das Metall
ist unmagnetisch.
Im Fall des Ytterbiums bedeutet das: In den meisten Verbindungen wie
auch in reinem Ytterbium-Metall besitzt Ytterbium die Valenz 2+. Damit
ist die 4f-Schale in der 4f14-Konfiguration abgeschlossen, Ytterbium
ist also unmagnetisch. Die zweite Möglichkeit ist die 4f13-Besetzung
des 4f-Niveaus. Ytterbium ist in diesem Fall dreiwertig (Valenz 3+) und
besitzt ein magnetisches Moment. Ebenso wird in einigen Ytterbium-Verbindungen
zwischenvalentes Verhalten beobachtet.
Der Kondo-Effekt
Der Kondo-Effekt [Kondo64]
beschreibt die Wechselwirkung zwischen magnetischen Störstellen und
Leitungselektronen: Die Spins der Leitungselektronen wechselwirken mit
dem magnetischen Moment der Störstelle. Die charakteristische Temperatur
dieser Wechselwirkung ist die Einzelionen-Kondotemperatur TK.
In den hier betrachteten Verbindungen tragen die 4f-Schalen der Lanthanidelemente
das magnetische Moment. Da die Selten-Erd-Ionen gitterperiodisch angeordnet
sind, spricht man von Kondo-Gitter-Systemen. Zu tiefen Temperaturen hin
wird die Kopplung der Leitungselektronen zunehmend stärker, und es
bildet sich ein kohärenter Zustand. Die stark lokalisierten magnetischen
Momente werden unterhalb der Kondo-Gitter-Temperatur T *
(der exakte Zusammenhang mit TK ist nicht geklärt)
immer mehr abgeschirmt. Es ist dadurch ein gänzlich unmagnetischer
Grundzustand möglich. Die Wechselwirkungsenergie ergibt sich aus einer
formalen Betrachtung:
.
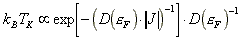Sie hängt exponentiell vom Produkt aus der Zustandsdichte an der
Fermikante und dem Betrag des Austauschintegrals J ab.
Die RKKY-Wechselwirkung
Die indirekte Austauschkopplung der lokalisierten magnetischen Momente
wird durch die RKKY-Wechselwirkung [Ruderman54]
beschrieben. Sie wird durch die Elektronen des Leitungsbandes vermittelt.
Sofern diese Wechselwirkung dominiert, führt sie zu magnetischer Ordnung.
Die charakteristische Energie ist proportional zu der Zustandsdichte an
der Fermikante und dem Quadrat des Austauschintegrals J:
.
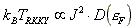Klassifizierung von Schwere-Fermionen-Systemen
In den intermetallischen Selten-Erd-Verbindungen treten der Kondo-Effekt
und die RKKY-Wechselwirkung in Konkurrenz zueinander. In dem von Grewe
und Steglich [Grewe91]
vorgestellen modifizierten Phasendiagramm nach Doniach [Doniach77]
werden sie durch die Kopplungskonstante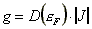 
verknüpft. Die Funktion
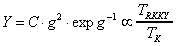
mit C = konstant beschreibt dabei deren Zusammenspiel: Für
g << 1 beobachtet man RKKY-Magnetismus mit stabilen Momenten,
angedeutet durch Y > 1. Im Bereich der Schweren Fermionen (g
< 1) ist Y von der Größenordnung 1. Man postuliert
einen itineranten Magnetismus der schweren Quasiteilchen. Für den
Fall g = 1 verschwindet die magnetische Ordnung und man vermutet
Nicht-Fermiflüssigkeits-Verhalten. Für g > 1 beobachtet
man Valenzfluktuationen und Fermiflüssigkeits-Verhalten. Fermiflüssigkeits-Verhalten
bedeutet dabei ein physikalisches Verhalten mit konstanten Werten von c
und C / T für T ®
0 K wie bei klassischen Metallen. Der elektrische Widerstand ist proportional
zu AT 2, wobei der Proportionalitätsfaktor A
mit g 2 skaliert. Nicht-Fermiflüssigkeits-Verhalten
bedeutet die Ungültigkeit dieser Beziehungen. Je nach zugrundeliegendem
Modell zeigt das System beispielsweise eine logarithmische Temperaturabhängigkeit
in c und C / T (und damit
eine logarithmische Divergenz von c0
und g ) sowie ein T 3/2-Gesetz
im elektrischen Widerstand.
